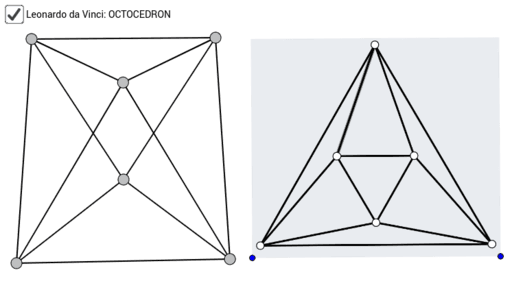
Octahedron Vertices

Octahedron Vertices Rating: 4,7/5 6506 votes
Given that I have the distance between the center of an octahedron and any of its faces (regular octahedron, so all the distances are equal), how can I calculate the coordinates of its vertices, considering that the octahedron may have rotation in any of the 3 Euler angles?
Geometry > Solid Geometry > Polyhedra > Platonic Solids >
Recreational Mathematics > Mathematical Art > Polyhedron Nets >
MathWorld Contributors > Singleton >
Less..The regular octahedron, often simply called 'the' octahedron, is the Platonic solid with six polyhedron vertices, 12 polyhedron edges, and eight equivalent equilateral triangular faces, denoted . It is also uniform polyhedron and Wenninger model . It is given by the Schläfli symbol and Wythoff symbol . The octahedron of unit side length is the antiprism of sides with height . The octahedron is also a square dipyramid with equal edge lengths.
The regular octahedron is implemented in the Wolfram Language as Octahedron[], and precomputed properties are available as PolyhedronData['Octahedron'].
There are 11 distinct nets for the octahedron, the same as for the cube (Buekenhout and Parker 1998). Questions of polyhedron coloring of the octahedron can be addressed using the Pólya enumeration theorem.
The dual polyhedron of an octahedron with unit edge lengths is a cube with edge lengths .
The illustration above shows an origami octahedron constructedfrom a single sheet of paper (Kasahara and Takahama 1987, pp. 60-61).
Like the cube, the regular octahedron has the octahedral group of symmetries.
The connectivity of the vertices is given by the octahedralgraph.
The regular octahedron has a single stellation: the stella octangula. The solid bounded by the two tetrahedra of the stella octangula (left figure) is a regular octahedron (right figure; Ball and Coxeter 1987).
S. Wagon (pers. comm., Oct. 30, 2013) has constructed a closed loop of eight regular octahedra.
The following table gives polyhedra which can be constructed by augmentation of a regular octahedron by pyramids of given heights .
| result | |
| small triakis octahedron | |
| 3 | stella octangula |
Three orientations of a regular octahedron are illustrated above. The left one has vertices , , , (for edge lengths ), the middle one has vertices , , (for edge lengths ), and the right one has vertices and (for edge lengths ).
In the former case, the face planes are , so a solid octahedron is given by the equation
If the edges of a regular octahedron are divided in the golden ratio such that the points of division for any face form an equilateral triangle, then the twelve points of division form an icosahedron (Wells 1991). In fact, there are two ways in which the edges can be internally divided in the golden ratio and two ways in which they can be externally divided, resulting in four possible icosahedra. Keeping the same connectivity, but reversing the long and short ends of the division gives Jessen's orthogonal icosahedron.
A plane perpendicular to a axis of an octahedron cuts the solid in a regular hexagonalcross section (Holden 1991, pp. 22-23). Since there are four such axes, there are four possible hexagonalcross sections.
The centers of the faces of a regular octahedron form a cube, and the centers of the faces of a cube form an octahedron (Steinhaus 1999, pp. 194-195). Faceted forms of the regular octahedron include the cubitruncated cuboctahedron and tetrahemihexahedron.
Let a regular octahedron be length on a side. The height of the top polyhedron vertex from the square plane is also the circumradius
where
Three new games are in the works for ninja-centric action series Senran Kagura, Famitsu magazine revealed in this week's issue (reported by ).Senran Kagura 2: Deep Crimson is currently in development for Nintendo 3DS from Tamsoft, the studio behind the brawler. The sequel will offer a similar style of side-scrolling 3D action and includes two male characters (a change from the usual roster of cleavage-heavy female designs.)The game will be joined by upcoming rhythm cooking game Dekamori Senran Kagura on PS Vita. According to, the title is categorized as a 'hyper big-breasted cooking-rhythm game,' so there's that niche filled. Senran kagura shinovi versus walkthrough.
is the diagonal length, so
Now compute the inradius.
(5) |
(7) |
so
Use similar triangles to obtain
(9) |
(11) |
so the inradius is
and twice the inradius gives the height of the octahedron viewed as a 3-sided antiprism. The midradius of the octahedron is
The area of one face of a regular octahedron is the areaof an equilateral triangle
The volume is two times the volume of a square-base pyramid,
The dihedral angle is
The regular octahedron can be built using a Haűyconstruction. The Haűy octahedral numbers
give another method for calculating the volume of theoctahedron,
in agreement with the result derived above.
SEE ALSO:Antiprism, Boat, Dürer's Solid, Escher's Solid, Haűy Construction, Icosahedron, Jumping Octahedron, Octahedral Graph, Octahedral Group, Octahedron, Octahedron 2-Compound, Octahedron 3-Compound, Octahedron 4-Compound, Octahedron 5-Compound, Octahedron 6-Compound, Octahedron 10-Compound, Platonic Solid, Polyhedron Coloring, Stella Octangula, Truncated OctahedronREFERENCES:Ball, W. W. R. and Coxeter, H. S. M. MathematicalRecreations and Essays, 13th ed. New York: Dover, 1987.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 228, 1987.
Buekenhout, F. and Parker, M. 'The Number of Nets of the Regular Convex Polytopes in Dimension .' Disc. Math.186, 69-94, 1998.
Cundy, H. and Rollett, A. 'Octahedron. .' §3.5.3 in Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., p. 64, 1989.
Davie, T. 'The Octahedron.' https://www.dcs.st-and.ac.uk/~ad/mathrecs/polyhedra/octahedron.html.
Geometry Technologies. 'Octahedron.' https://www.scienceu.com/geometry/facts/solids/octa.html.
Harris, J. W. and Stocker, H. 'Octahedron.' §4.4.4 in Handbook of Mathematics and Computational Science. New York: Springer-Verlag, p. 100, 1998.
Holden, A. Shapes,Space, and Symmetry. New York: Dover, 1991.
Kasahara, K. Origami Omnibus: Paper-Folding for Everyone. Tokyo: Japan Publications, p. 204, 1988.
Kasahara, K. and Takahama, T. Origamifor the Connoisseur. Tokyo: Japan Publications, 1987.
Steinhaus, H. MathematicalSnapshots, 3rd ed. New York: Dover, pp. 193-195, 1999.
Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, p. 163, 1991.
Wenninger, M. J. 'The Octahedron.' Model 2 in PolyhedronModels. Cambridge, England: Cambridge University Press, p. 15, 1989.
CITE THIS AS:Weisstein, Eric W. 'Regular Octahedron.'From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/RegularOctahedron.html